Kronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix multiplication, which is an entirely different operation. It is named after German mathematician Leopold Kronecker.
Contents |
Definition
If A is an m-by-n matrix and B is a p-by-q matrix, then the Kronecker product A ⊗ B is the mp-by-nq block matrix 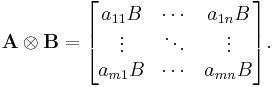
More explicitly, we have
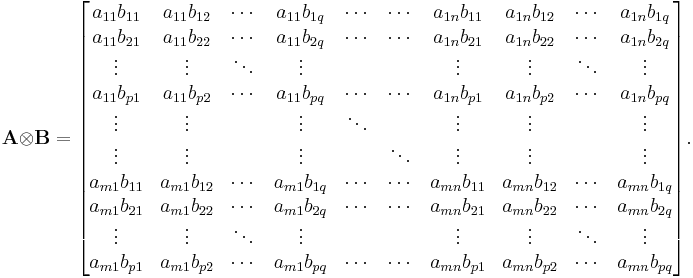
If A and B represent linear transformations V1 → W1 and V2 → W2, respectively, then A ⊗ B represents the tensor product of the two maps, V1 ⊗ V2 → W1 ⊗ W2.
Examples
 .
.
Properties
Bilinearity and associativity
The Kronecker product is a special case of the tensor product, so it is bilinear and associative:
where A, B and C are matrices and k is a scalar.
The Kronecker product is not commutative: in general, A  B and B
B and B  A are different matrices. However, A
A are different matrices. However, A  B and B
B and B  A are permutation equivalent, meaning that there exist permutation matrices P and Q such that
A are permutation equivalent, meaning that there exist permutation matrices P and Q such that
If A and B are square matrices, then A  B and B
B and B  A are even permutation similar, meaning that we can take P = QT.
A are even permutation similar, meaning that we can take P = QT.
The mixed-product property
If A, B, C and D are matrices of such size that one can form the matrix products AC and BD, then
This is called the mixed-product property, because it mixes the ordinary matrix product and the Kronecker product. It follows that A  B is invertible if and only if A and B are invertible, in which case the inverse is given by
B is invertible if and only if A and B are invertible, in which case the inverse is given by
Transpose
The operation of transposition is distributive over the Kronecker product:
Kronecker sum and exponentiation
If A is n-by-n, B is m-by-m and 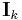 denotes the k-by-k identity matrix then we can define what is sometimes called the Kronecker sum,
denotes the k-by-k identity matrix then we can define what is sometimes called the Kronecker sum,  , by
, by
(Note that this is different from the direct sum of two matrices.) This operation is related to the tensor product on Lie algebras.
We have the following formula for the matrix exponential which is useful in the numerical evaluation of certain continuous-time Markov processes ,
Kronecker sums appear naturally in physics when considering ensembles of non-interacting systems. Let 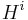 be the Hamiltonian of the i-th such system. Then the total Hamiltonian of the ensemble is
be the Hamiltonian of the i-th such system. Then the total Hamiltonian of the ensemble is 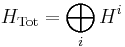 .
.
Spectrum
Suppose that A and B are square matrices of size n and m respectively. Let λ1, ..., λn be the eigenvalues of A and μ1, ..., μm be those of B (listed according to multiplicity). Then the eigenvalues of A  B are
B are
It follows that the trace and determinant of a Kronecker product are given by
Singular values
If A and B are rectangular matrices, then one can consider their singular values. Suppose that A has rA nonzero singular values, namely
Similarly, denote the nonzero singular values of B by
Then the Kronecker product A  B has rArB nonzero singular values, namely
B has rArB nonzero singular values, namely
Since the rank of a matrix equals the number of nonzero singular values, we find that
Relation to the abstract tensor product
The Kronecker product of matrices corresponds to the abstract tensor product of linear maps. Specifically, if the vector spaces V, W, X, and Y have bases {v1, ... , vm}, {w1, ... , wn}, {x1, ... , xd}, and {y1, ... , ye}, respectively, and if the matrices A and B represent the linear transformations S : V → X and T : W → Y, respectively in the appropriate bases, then the matrix A ⊗ B represents the tensor product of the two maps, S ⊗ T : V ⊗ W → X ⊗ Y with respect to the basis {v1 ⊗ w1, v1 ⊗ w2, ... , v2 ⊗ w1, ... , vm ⊗ wn} of V ⊗ W and the similarly defined basis of X ⊗ Y with the property that A ⊗ B(vi ⊗ wj) = (Avi)⊗(Bwj), where i and j are integers in the proper range.[1]
When V and W are Lie algebras, and S : V → V and T : W → W are Lie algebra homomorphisms, the Kronecker sum of A and B represents the induced Lie algebra homomorphisms V ⊗ W → V ⊗ W.
Relation to products of graphs
The Kronecker product of the adjacency matrices of two graphs is the adjacency matrix of the tensor product graph. The Kronecker sum of the adjacency matrices of two graphs is the adjacency matrix of the Cartesian product graph. See,[2] answer to Exercise 96.
Matrix equations
The Kronecker product can be used to get a convenient representation for some matrix equations. Consider for instance the equation AXB = C, where A, B and C are given matrices and the matrix X is the unknown. We can rewrite this equation as
Here, vec(X) denotes the vectorization of the matrix X formed by stacking the columns of X into a single column vector. It now follows from the properties of the Kronecker product that the equation AXB = C has a unique solution if and only if A and B are nonsingular (Horn & Johnson 1991, Lemma 4.3.1).
If X is row-ordered into the column vector x then 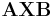 can be also be written as
can be also be written as 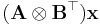 (Jain 1989, 2.8 Block Matrices and Kronecker Products)
(Jain 1989, 2.8 Block Matrices and Kronecker Products)
History
The Kronecker product is named after Leopold Kronecker, even though there is little evidence that he was the first to define and use it. Indeed, in the past the Kronecker product was sometimes called the Zehfuss matrix, after Johann Georg Zehfuss.
Related matrix operations
Two related matrix operations are the Tracy-Singh and Khatri-Rao products which operate on partitioned matrices. Let the m-by-n matrix A be partitioned into the 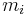 -by-
-by-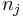 blocks
blocks 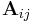 and
and  -by-
-by- matrix
matrix 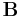 into the
into the 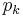 -by-
-by-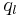 blocks Bkl with of course
blocks Bkl with of course 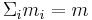 ,
, 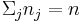 ,
, 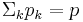 and
and 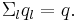
The Tracy-Singh product[3][4] is defined as
which means that the 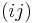 th subblock of the mp-by-nq product
th subblock of the mp-by-nq product 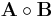 is the
is the 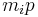 -by-
-by-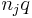 matrix
matrix 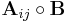 , of which the
, of which the 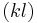 th subblock equals the
th subblock equals the 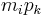 -by-
-by-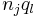 matrix
matrix  . Essentially the Tracy-Singh product is the pairwise Kronecker product for each pair of partitions in the two matrices.
. Essentially the Tracy-Singh product is the pairwise Kronecker product for each pair of partitions in the two matrices.
For example, if A and B both are 2-by-2 partitioned matrices e.g.:
we get:
The Khatri-Rao product[5][6] is defined as
in which the 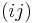 th block is the
th block is the 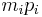 -by-
-by-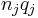 sized Kronecker product of the corresponding blocks of
sized Kronecker product of the corresponding blocks of 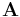 and
and 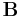 , assuming the number of row and column partitions of both matrices is equal. The size of the product is then
, assuming the number of row and column partitions of both matrices is equal. The size of the product is then 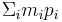 -by-
-by-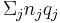 . Proceeding with the same matrices as the previous example we obtain:
. Proceeding with the same matrices as the previous example we obtain:
This is a submatrix of the Tracy-Singh product of the two matrices (each partition in this example is a partition in a corner of the Tracy-Singh product).
A column-wise Kronecker product of two matrices may also be called the Khatri-Rao product. This product assumes the partitions of the matrices are their columns. In this case 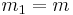 ,
, 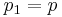 ,
, 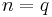 and
and 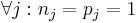 . The resulting product is a
. The resulting product is a 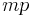 -by-
-by- matrix of which each column is the Kronecker product of the corresponding columns of
matrix of which each column is the Kronecker product of the corresponding columns of  and
and  . Using the matrices from the previous examples with the columns partitioned:
. Using the matrices from the previous examples with the columns partitioned:
so that:
See also
Notes
- ^ Pages 401–402 of Dummit, David S.; Foote, Richard M. (1999), Abstract Algebra (2 ed.), New York: John Wiley and Sons, Inc., ISBN 0-471-36857-1
- ^ D. E. Knuth: "Pre-Fascicle 0a: Introduction to Combinatorial Algorithms", zeroth printing (revision 2), to appear as part of D.E. Knuth: The Art of Computer Programming Vol. 4A
- ^ Tracy, DS, Singh RP. 1972. A new matrix product and its applications in matrix differentiation. Statistica Neerlandica 26: 143–157.
- ^ Liu S. 1999. Matrix results on the Khatri-Rao and Tracy-Singh products. Linear Algebra and its Applications 289: 267–277. (pdf)
- ^ Khatri C. G., C. R. Rao (1968), "Solutions to some functional equations and their applications to characterization of probability distributions", Sankhya 30: 167–180, http://sankhya.isical.ac.in/search/30a2/30a2019.html.
- ^ Zhang X, Yang Z, Cao C. (2002), "Inequalities involving Khatri-Rao products of positive semi-definite matrices", Applied Mathematics E-notes 2: 117–124.
References
- Horn, Roger A.; Johnson, Charles R. (1991), Topics in Matrix Analysis, Cambridge University Press, ISBN 0-521-46713-6.
- Jain, Anil K. (1989), Fundamentals of Digital Image Processing, Prentice Hall, ISBN 0-13-336165-9.
- Steeb, Willi-Hans (1997), Matrix Calculus and Kronecker Product with Applications and C++ Programs, World Scientific Publishing, ISBN 9810232411
- Steeb, Willi-Hans (2006), Problems and Solutions in Introductory and Advanced Matrix Calculus, World Scientific Publishing, ISBN 9812569162
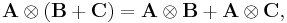
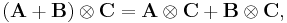
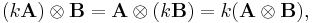
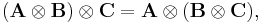
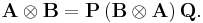
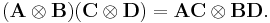
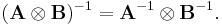
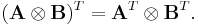
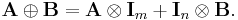
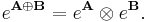
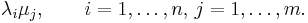
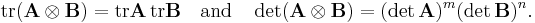
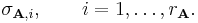
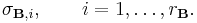

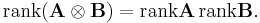
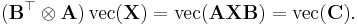
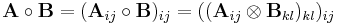
![\mathbf{A} =
\left[
\begin{array} {c | c}
\mathbf{A}_{11} & \mathbf{A}_{12} \\
\hline
\mathbf{A}_{21} & \mathbf{A}_{22}
\end{array}
\right]
=
\left[
\begin{array} {c c | c}
1 & 2 & 3 \\
4 & 5 & 6 \\
\hline
7 & 8 & 9
\end{array}
\right]
,\quad
\mathbf{B} =
\left[
\begin{array} {c | c}
\mathbf{B}_{11} & \mathbf{B}_{12} \\
\hline
\mathbf{B}_{21} & \mathbf{B}_{22}
\end{array}
\right]
=
\left[
\begin{array} {c | c c}
1 & 4 & 7 \\
\hline
2 & 5 & 8 \\
3 & 6 & 9
\end{array}
\right]
,](/2012-wikipedia_en_all_nopic_01_2012/I/6ab8097e6617ec07d5d35bf7c55b7bd0.png)
![\mathbf{A} \circ \mathbf{B} =
\left[
\begin{array} {c | c}
\mathbf{A}_{11} \circ \mathbf{B} & \mathbf{A}_{12} \circ \mathbf{B} \\
\hline
\mathbf{A}_{21} \circ \mathbf{B} & \mathbf{A}_{22} \circ \mathbf{B}
\end{array}
\right]
=
\left[
\begin{array} {c | c | c | c }
\mathbf{A}_{11} \otimes \mathbf{B}_{11} & \mathbf{A}_{11} \otimes \mathbf{B}_{12} & \mathbf{A}_{12} \otimes \mathbf{B}_{11} & \mathbf{A}_{12} \otimes \mathbf{B}_{12} \\
\hline
\mathbf{A}_{11} \otimes \mathbf{B}_{21} & \mathbf{A}_{11} \otimes \mathbf{B}_{22} & \mathbf{A}_{12} \otimes \mathbf{B}_{21} & \mathbf{A}_{12} \otimes \mathbf{B}_{22} \\
\hline
\mathbf{A}_{21} \otimes \mathbf{B}_{11} & \mathbf{A}_{21} \otimes \mathbf{B}_{12} & \mathbf{A}_{22} \otimes \mathbf{B}_{11} & \mathbf{A}_{22} \otimes \mathbf{B}_{12} \\
\hline
\mathbf{A}_{21} \otimes \mathbf{B}_{21} & \mathbf{A}_{21} \otimes \mathbf{B}_{22} & \mathbf{A}_{22} \otimes \mathbf{B}_{21} & \mathbf{A}_{22} \otimes \mathbf{B}_{22}
\end{array}
\right]](/2012-wikipedia_en_all_nopic_01_2012/I/8acac848b16ae6f80d5ffcdb6e493833.png)
![=
\left[
\begin{array} {c c | c c c c | c | c c}
1 & 2 & 4 & 7 & 8 & 14 & 3 & 12 & 21 \\
4 & 5 & 16 & 28 & 20 & 35 & 6 & 24 & 42 \\
\hline
2 & 4 & 5 & 8 & 10 & 16 & 6 & 15 & 24 \\
3 & 6 & 6 & 9 & 12 & 18 & 9 & 18 & 27 \\
8 & 10 & 20 & 32 & 25 & 40 & 12 & 30 & 48 \\
12 & 15 & 24 & 36 & 30 & 45 & 18 & 36 & 54 \\
\hline
7 & 8 & 28 & 49 & 32 & 56 & 9 & 36 & 63 \\
\hline
14 & 16 & 35 & 56 & 40 & 64 & 18 & 45 & 72 \\
21 & 24 & 42 & 63 & 48 & 72 & 27 & 54 & 81
\end{array}
\right].](/2012-wikipedia_en_all_nopic_01_2012/I/ec1f1b7a7efefc8af060e7d9a5e1539f.png)
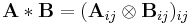
![\mathbf{A} \ast \mathbf{B} =
\left[
\begin{array} {c | c}
\mathbf{A}_{11} \otimes \mathbf{B}_{11} & \mathbf{A}_{12} \otimes \mathbf{B}_{12} \\
\hline
\mathbf{A}_{21} \otimes \mathbf{B}_{21} & \mathbf{A}_{22} \otimes \mathbf{B}_{22}
\end{array}
\right]
=
\left[
\begin{array} {c c | c c}
1 & 2 & 12 & 21 \\
4 & 5 & 24 & 42 \\
\hline
14 & 16 & 45 & 72 \\
21 & 24 & 54 & 81
\end{array}
\right].](/2012-wikipedia_en_all_nopic_01_2012/I/1e705fe0428a16d4c5223bd38a6b8917.png)
![\mathbf{C} =
\left[
\begin{array} { c | c | c}
\mathbf{C}_1 & \mathbf{C}_2 & \mathbf{C}_3
\end{array}
\right]
=
\left[
\begin{array} {c | c | c}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{array}
\right]
,\quad
\mathbf{D} =
\left[
\begin{array} { c | c | c }
\mathbf{D}_1 & \mathbf{D}_2 & \mathbf{D}_3
\end{array}
\right]
=
\left[
\begin{array} { c | c | c }
1 & 4 & 7 \\
2 & 5 & 8 \\
3 & 6 & 9
\end{array}
\right]
,](/2012-wikipedia_en_all_nopic_01_2012/I/de6098c1671347db8bb6925163f5179f.png)
![\mathbf{C} \ast \mathbf{D}
=
\left[
\begin{array} { c | c | c }
\mathbf{C}_1 \otimes \mathbf{D}_1 & \mathbf{C}_2 \otimes \mathbf{D}_2 & \mathbf{C}_3 \otimes \mathbf{D}_3
\end{array}
\right]
=
\left[
\begin{array} { c | c | c }
1 & 8 & 21 \\
2 & 10 & 24 \\
3 & 12 & 27 \\
4 & 20 & 42 \\
8 & 25 & 48 \\
12 & 30 & 54 \\
7 & 32 & 63 \\
14 & 40 & 72 \\
21 & 48 & 81
\end{array}
\right].](/2012-wikipedia_en_all_nopic_01_2012/I/184a20bee0ae59a65220a34b59173c9f.png)